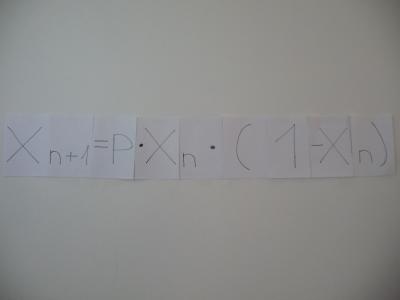Im Begleitprogramm erklärte der Mathematikfachmann Hartmut Haker am Samstag, 23. April anschaulich das Motiv der Einladungskarte und des Plakates der Ausstellung, das Ljapunov-Diagramm. Dabei leitete er mathematisch anhand dieses Diagrammes den Umsprung von geordneten zu chaotischen Zuständen her:

Einen schönen guten Abend!
Mein Name ist Hartmut Haker.
Ich bin Mathematik-Fachmann und wurde eingeladen, Ihnen das Motiv der Einladungskarte und des Plakates dieser Ausstellung zu erklären.
Das Ljapunov-Diagramm, das Sie hier an der Wand sehen.

Das Thema dieser Ausstellung ist absolut aktuell der „Fortschritt“, der unsere Welt bewegt.
Es herrscht allgemein der Glaube, dass sich die Gesellschaft mit dem Wissenszuwachs und den daraus resultierenden Technologien unaufhaltsam auf einen utopischen Zustand zubewegen werde.
Alles wird schneller, weiter und höher.
Sehen Sie hinter dem Pfeiler den „Burj Dubai“, das momentan höchste Hochhaus und aktuellste Fortschrittsymbol, über 850 Meter hoch. Der Fortschritt schreitet meterweise fort und versucht die alten Maßstäbe zu toppen.

Bekanntlich hat jeder Fortschritt auch negative Auswirkungen. Aktuell an der Kernenergie, der Katastrophe in Japan, und der Gentechnik lässt sich die Ambivalenz des Fortschritts aufzeigen.
Und jetzt erkläre ich Ihnen den Umsprung von geordneten zu chaotischen Zuständen nach dem Ljapunov-Diagramm.
Die Chaostheorie deckt ganz erstaunliche Konstruktions- und Bewegungsprinzipien von Natur und Gesellschaft auf. Sie klärt darüber auf, warum Ordnung wie zufällig wieder in Unordnung umkippen kann.

Ordnende Kräfte können auch Unordnung hervorrufen, und das um so mehr, je komplexer die zu ordnenden Systeme sind.
Die Chaosforschung kommt bei Systemen zur Anwendung, die chaotisches Verhalten zeigen können.
In der Medizin wird damit die Entstehung von Tumoren und der Ausfall bestimmter Hirnfunktionen beim Schlaganfall erforscht.
Auch Börsenkurse, Konjunkturentwicklungen und Erklärungen von politischen und wirtschaftlichen Krisen können mittels der Chaosforschung betrachtet werden.
Der russische Mathematiker Ljapunov hatte die Idee, ein Maß für das Chaos in einer Iteration zu entwickeln.
Iteration ist eine Methode, sich der exakten Lösung eines Rechenproblems schrittweise, aber zielgerichtet anzunähern.
Sie besteht in der wiederholten Anwendung des selben Rechenverfahrens, wie Sie gleich am Beispiel sehen können.
Die Ljapunov-Diagramme werden aus der gewöhnlichen logistischen Gleichung gewonnen, die mit einem Parameter p versehen ist.
xn+1 = p * xn * (1 - xn)
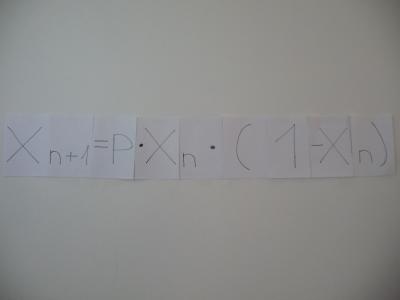
Parameter sind nur für einen gerade betrachteten Fall konstant, für den nächsten Fall können sie aber variiert werden.
Der Parameter p wird bei jedem Iterationsschritt (xn+1) durch den vorherigen xn-Wert variiert.
Aus der Folge der iterierten Punkte xn kann nun der sogenannte Ljapunov-Exponent berechnet werden.
Dieser gibt an, ob die Punktfolge periodisches oder chaotisches Verhalten zeigt. Ist die Folge chaotisch wird der Punkt grau eingefärbt. Bei periodischem Verhalten hingegen ist die verwendete Farbpalette grün.

Das Diagramm ist also sozusagen eine Landkarte, anhand der das dynamische Verhalten von Iterationsgleichungen betrachtet werden kann.
Am Beispiel der Berechnung der Geburtenrate, das heißt, wie viele Kinder eine Frau in ihrem Leben im Durchschnitt bekommt, möchte ich Ihnen die Entwicklung des Diagrammes zeigen.

Weltweit beträgt die Geburtenrate im Schnitt 2,6 Kinder pro Frau.
In Entwicklungsländern liegt sie bei 4,8.
In den westlichen Ländern bekommt eine Frau nur 1,6 Kinder in ihrem Leben – das heißt, dass hier die Bevölkerung stetig sinken wird.
p ist immer eine positive Zahl, sie gibt die angenommene gedachte konstante Geburtenrate an.
xn ist dabei eine Zahl zwischen 0 und 1. Sie repräsentiert die Geburtenrate im Jahr n.
Die Zahl x0 steht also für die Startgeburtenrate(im Jahr 0). Für x0 nehmen wir x0 = 0,8 an. Das bedeutet eine Rate von 80 %.
In unserem Fall nehmen wir verschiedene p-Werte an, die die Entwicklung zum Chaos zeigen.

Natürlich gibt es unendlich viele Kombinationsmöglichkeiten in der Annahme des p- und des x0-Wertes.
Nehmen wir einen p-Wert von 0,5 an, das heißt, die angenommene konstante Geburtenrate liegt bei 0,5, jede Frau bekommt nur 0,5 Kinder in ihrem Leben.
Dazu zeichne ich ein Diagramm, das noch nicht das Ljapunov-Diagramm ist. Dabei ist die x-Achse die Zeit, also die betrachteten Jahre. Die y-Achse ist xn, das heißt das Ergebnis der jeweiligen Iteration. Die erreichte Geburtenrate in jedem Jahr. Für x0 hatten wir 0,8 angenommen. Im Jahre null beträgt die Geburtenrate also 80 % von der angenommenen Geburtenrate p = 0,5.

Folgende, sehr niedrige Ergebnisse kommen für die ersten vier betrachteten Jahre zustande:
x0 = 0,8, x1 = 0,08, x2 = 0,04, x3 = 0,02, x4 = 0,01
Der Trend bei dieser sehr geringen Geburtenrate geht dahin, dass nach einigen Jahren die Geburtenrate auf null sinkt, die Bevölkerung also aussterben wird.
Ljapunov hat angenommen, dass bei periodischem Verhalten, was hier der Fall ist – die Werte sinken gleichmäßig ab – Ordnung herrscht. Im Ljapunov-Diagramm würde für diese Punkte die Farbe grün gewählt werden.
Dazu zeichne ich das Ljapunov-Diagramm, wobei für verschiedene Fälle andere Formen entstehen, das Prinzip ist aber dasselbe.
Nun ist die y-Achse der xn-Wert des betrachteten Jahres und die x-Achse der xn-Wert des darauf folgenden Jahres. Ich trage alle Werte ein. Da für p = 0,5 Ordnung herrscht, sind alle errechneten Punkte grün.
Als Nächstes nehmen wir einen p-Wert von 1,5 an, das heißt, die angenommene konstante Geburtenrate liegt bei 1,5, jede Frau bekommt 1,5 Kinder in ihrem Leben.
Dazu zeichne ich wieder ein Diagramm mit der x-Achse als Zeit und die y-Achse ist xn, das heißt das Ergebnis der jeweiligen Iteration. Die erreichte Geburtenrate in jedem Jahr. Für x0 hatten wir 0,8 angenommen - die Geburtenrate liegt bei 80 % von der angenommenen Geburtenrate p = 1,5.
Folgende Ergebnisse kommen für die ersten fünf betrachteten Jahre zustande:
x0 = 0,8, x1 = 0,24, x2 = 0,27, x3 = 0,29, x4 = 0,31, x5 = 0,32
Der Trend bei dieser recht geringen Geburtenrate geht dahin, dass nach einigen Jahren die Geburtenrate auf einem geringen Stand gleich bleibt.
Auch hier liegt periodisches Verhalten vor – es herrscht Ordnung. Im Ljapunov-Diagramm wird für diese Punkte die Farbe grün gewählt.
Wieder trage ich die Punkte im Ljapunov-Diagramm ein. Nun ist die y-Achse der xn-Wert des betrachteten Jahres und die x-Achse der xn-Wert des darauf folgenden Jahres. Da für p = 1,5 Ordnung herrscht, sind alle errechneten Punkte grün.
Ab dem p-Wert von 3,57 an, das heißt, die angenommene konstante Geburtenrate liegt bei 3,57, jede Frau bekommt 3,57 Kinder in ihrem Leben, fängt das Chaos an. Die Erklärung liegt in der Unüberschaubarkeit von zu großen Systemen. Die Werte der betrachteten Jahre springen hin und her.

Folgende Ergebnisse kommen für die ersten acht betrachteten Jahre zustande:
x0 = 0,8, x1 = 0,57, x2 = 0,88, x3 = 0,39, x4 = 0,85, x5 = 0,46, x6 = 0,88, x7 = 0,36, x8 = 0,82
Der Trend bei dieser recht hohen Geburtenrate geht dahin, dass die Werte der betrachteten Jahre hin und her springen.
Hier liegt chaotisches Verhalten vor. Im Ljapunov-Diagramm wird für diese Punkte die Farbe grau gewählt werden.
Über einem p-Wert von 3,57 setzt sich dieses chaotische Verhalten fort.
Wenn ich nun ungefähr im Diagramm die Grenze zwischen Chaos und Ordnung ziehe, ist ungefähr die Form des Ljapunovs-Diagramms zu erkennen. Wie gesagt, können für verschiedene Ausgangswerte und Fälle andere Formen des Diagrammes erreicht werden.
Im Ljapunov-Diagramm fällt auf, dass am Rand der Übergang zwischen geordnetem Verhalten und Chaos recht ausgefranst ist. In der Tat gibt es Regionen, in denen sich Ordnung und Chaos sehr nahe kommen.
Jedenfalls ist ersichtlich, dass bei Ausuferungen und fehlender Überschaubarkeit von Systemen Chaos entsteht.
Und so ist es auch mit dem Fortschritt. Ein höher, schneller, weiter mag zwar das Leben scheinbar erleichtern, kann aber, wie wir es in Fukushima und auch an unserem Hauptbahnhof sehen, zu unüberschaubaren Prozessen führen.
Das wars zum Chaos.
Vielleicht haben Sie dazu noch eine Frage an mich oder möchten etwas zum Chaos sagen.
Im Anschluss können Sie hier den Film „Fausto 5.0“ der freien, international bekannten katalanischen Performance- und Theatergruppe La Fura dels Baus erleben.
Vielen Dank für Ihre Aufmerksamkeit und einen schönen Abend!
urbane visionen - 25. Apr, 11:35